为了将计算结果进行可视化呈现,MATLAB提供了诸多绘图功能,可以满足不同可视化的需求。这篇内容将主要介绍使用MATLAB进行二维绘图的入门操作。
plot函数
提到MATLAB中的二维绘图函数,那一定要提到plot函数。虽然是最基础的二维绘图函数,但是其功能却十分的强大。在开始绘图的学习之前,请先将下面这句话默念3遍:
MATLAB主要用来处理【数值运算】!
这句话虽然不完全正确,但在初学阶段请牢记。如同之前提到的,MATLAB的主要运算对象是【矩阵】,因此MATLAB的绘制实际上是根据你提供的数据进行绘图,换句话说你可以当作MATLAB是个不认识函数的“傻子”。举个栗子,你让MATLAB绘制所谓y=sin(x)的图像,它做不到;但是根据产生的x、y值序列,MATLAB可以轻松进行绘图。
plot函数的基本使用方法
plot函数可以根据提供的数据绘制对应的图像,其基本用法如下:
% 以1:n为X坐标,绘制Y值的折线图
plot(Y)
% 根据提供的X和Y数据绘制折线图
plot(X, Y)
% 绘制折线图并指定线型、颜色等特征
plot(X, Y, LineSpec)
% 在同一幅图中绘制多组图线
plot(X1, Y1, LineSpec1, Xn, Yn, LineSpecn)
例如我们绘制函数y=sin(x)在区间[0,5]上的图像,可以使用以下的代码:
% 产生x值数据,这里每隔0.1取一个点。
x = 0:0.1:5;
% 根据函数关系,生成对应的y值数据;MATLAB提供的sin函数支持对向量的处理。
y = sin(x);
% 绘图,选择曲线为红色
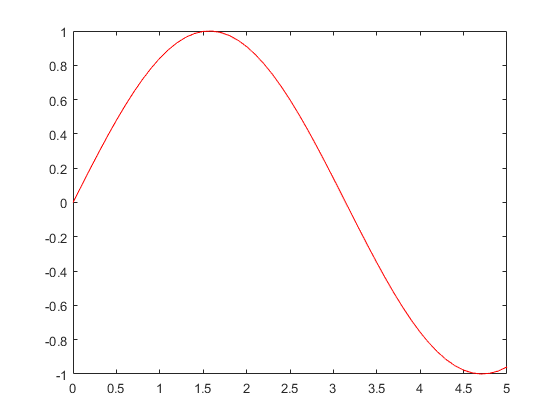
plot(x, y, 'r');
绘图结果如图所示:
同时绘制y=x^2和y=0.5x^3两个图像:
% 产生x值数据,这里每隔0.1取一个点。
x = 0:0.1:5;
% 根据函数关系,生成对应的y值数据。
y1 = x.^2;
y2 = 0.5 * x.^3;
% 绘图
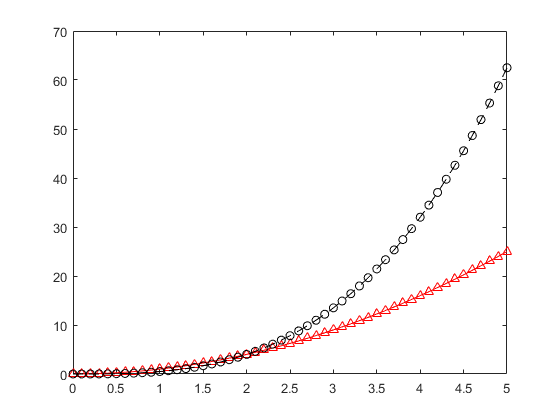
plot(x, y1, 'r^-', x, y2, 'ko--');
绘图结果:
常见的颜色、线型、标记点属性如下:
| 颜色 | 符号 |
|---|---|
| 红色 | ‘r’ |
| 粉红 | ‘m’ |
| 绿色 | ‘g’ |
| 青色 | ‘c’ |
| 蓝色 | ‘b’ |
| 白色 | ‘w’ |
| 黄色 | ‘y’ |
| 黑色 | ‘k’ |
| 线型 | 符号 |
|---|---|
| 实线 | ’-‘ |
| 虚线 | ’–’ |
| 点线 | ’:’ |
| 点划线 | ’-.’ |
| 标记点类型 | 符号 |
|---|---|
| 上三角 | ’^’ |
| 下三角 | ‘v’ |
| 左三角 | ’<’ |
| 右三角 | ’>’ |
| 星号 | ‘*’ |
| 加号 | ’+’ |
| 叉号 | ‘x’ |
| 实心圆 | ’.’ |
| 空心圆 | ‘o’ |
| 正方形 | ’s’ |
| 五角星 | ‘p’ |
| 六角星 | ‘h’ |
| 菱形 | ‘d’ |
这些属性可以仅指定一种,也可以被同时指定,指定时无需区分顺序。需要注意的是如果指定了标记点类型的话,必须要进一步指定线型,否则绘图时只会出现标记点而没有线。
plot函数的额外属性
使用plot函数除了可以对颜色、线型、标记点类型进行修改外,还可以通过以下方式设定通用属性值:
plot(X, Y, LineSpec, Name, Value)
常见的属性值包括
| 属性名 | 说明 |
|---|---|
| ‘LineWidth’ | 线宽(默认为0.5) |
| ‘MarkerSize’ | 标记点大小(默认为6.0) |
| ‘MarkerEdgeColor’ | 标记点轮廓颜色(与线颜色写法相同) |
| ‘MarkerFaceColor’ | 标记点填充颜色(与线颜色写法相同) |
例如下面代码设置了多种参数:
x = -pi:pi/10:pi;
y = tan(sin(x)) - sin(tan(x));
plot(x,y,'--gs',...
'LineWidth',2,...
'MarkerSize',10,...
'MarkerEdgeColor','b',...
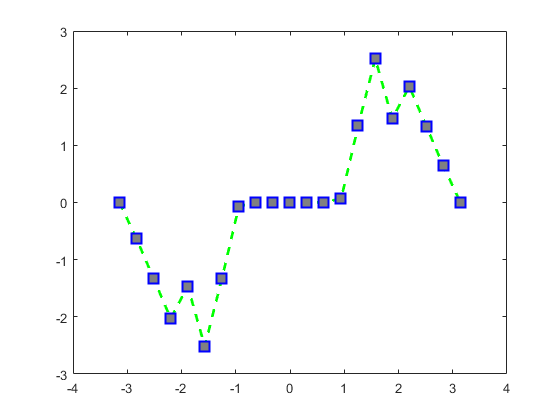
'MarkerFaceColor',[0.5,0.5,0.5])
绘制出的图像如下所示:
添加/设置图像其他部分
一张完整的图表应当包括标题、轴坐标等元素。下面展示了一些常用的添加/设置图表元素的方法。
% 设置图表标题
title('Sample Title');
% 设置x坐标轴名称
xlabel('X Label Title');
% 设置y坐标轴名称
ylabel('Y Label Title');
% 设置图例项
legend('Legend1','Legend2','LegendN');
% 设置X、Y轴坐标范围
xlim([XMIN, XMAX]);
ylim([YMIN, YMAX]);
% 或者使用以下方式设置坐标范围
axis([XMIN, XMAX, YMIN, YMAX]);
% 开启网格
grid on
使用代码对图像进行调整,可以使得每次生成的图像具有相同的属性。但是还有一种更加交互化(福利化)的方式,那就是在图像界面进行直接设置。在生成的图像中选择“编辑”->“图形属性”,即可打开对应的交互化设置界面。点击图中的坐标轴、图线还可以对这些元素进行对应的设置。
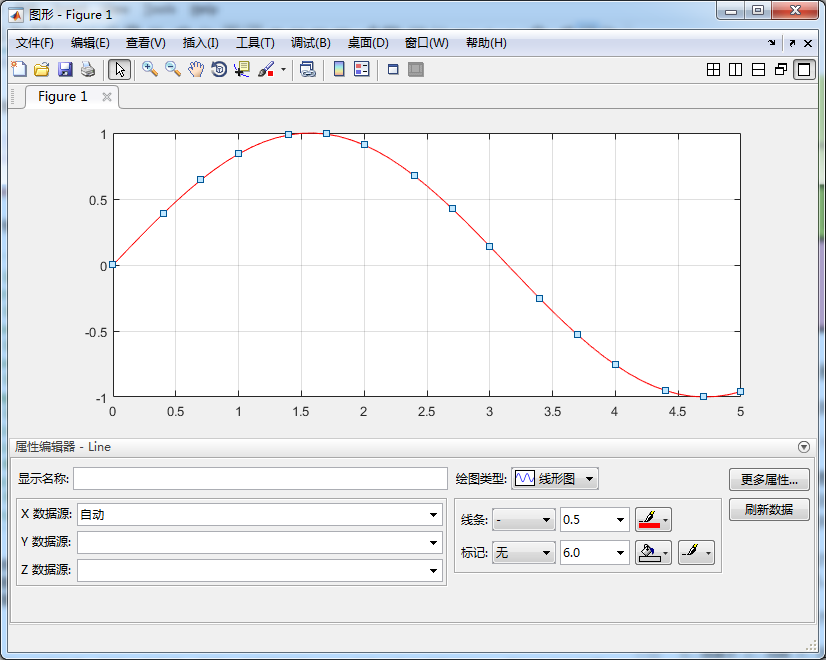
新建图像和添加图像
当你想要绘制多张图像时,你可能会发现多次调用plot方法会使得后一次绘制的结果覆盖已有的图像。为了生成新的图像,需要使用以下命令生成一张空白的图像。
figure;
事实上,在你第一次调用plot()函数时,你可以认为MATLAB已经自动调用了figure方法,生成新的空白图像用于绘图。但之后若没有再次调用figure方法,则每次使用plot()时将覆盖已有的图像。
例如使用以下代码生成互为反函数的y=ln(x)和y=e^x的两幅图像:
x = 0.1:0.1:5;
y = log(x);
figure; % 第一次绘制时,figure命令可省略
% 绘制函数y=ln(x)的图像
plot(x, y);
title('函数y=ln(x)');
figure;
% 绘制函数y=e^x的图像
plot(y, x);
title('函数y=e^x');
Matlab会生成两幅图像:
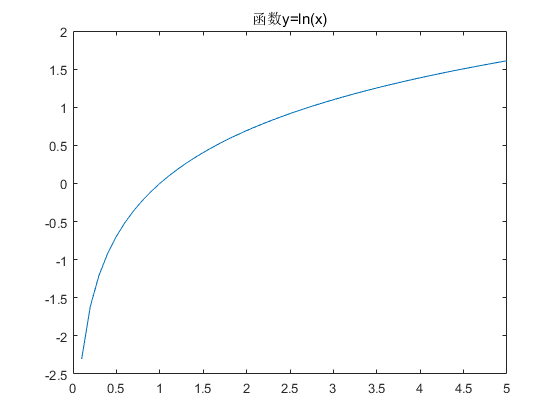
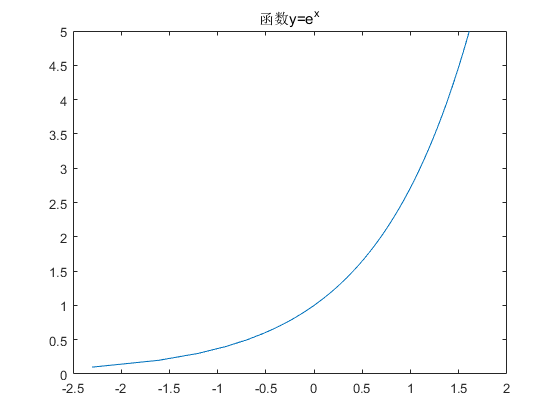
有时我们可能并不想将结果绘制在多个图像上,而是直接绘制在同一个图像上。但是多次使用plot()函数又会使得之前的图像被覆盖,这时就需要使用hold on命令来保持当前图像。
hold on命令的使用方法如下:
plot();
hold on;
plot();
需要注意的是,使用hold on命令之后,两次的plot将完全不相关,等同于在一次plot()函数中同时绘制多组数据。因此使用对于plot()函数出现的多条图线,将不会自动生成直线连接它们。
使用hold on方法可以使我们绘制图像时不拘泥于将绘图数据全部计算完成后画出,而是使用“更新”的方法进行绘图。例如绘制幂函数y=x^a在不同a值时的函数图像:
figure; % 第一次绘制时,figure命令可省略
for a = -2:2
x = -2:0.1:2;
y = x .^ a;
plot(x, y, 'linewidth', 1);
hold on;
end
grid on;
axis([-2,2,-5,5]);
title('y=x^a在不同a值下的图像');
legend('a=-2', 'a=-1', 'a=0', 'a=1', 'a=2');
绘制在同一幅图中的效果:
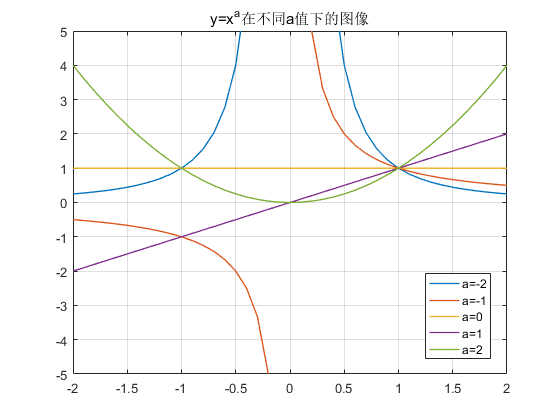
利用hold on还可以作出类似“动态变化”的效果(关于“水滴数”可以参考第4篇教程中的介绍):
% “水滴数”动态变化图
% 设置初始值
num = 50;
% 设置刷新时间
refresh = 0.5;
% 记录迭代次数
iter = 1;
% 进行第一次绘图,这里我们采用散点图,并添加标题等其他元素
figure; % 第一次绘制图像的时候,是否添加这句话效果相同
plot(iter, num, 'ro');
axis([1, 25, 0, 100]);
title('“水滴数”动态变化展示');
xlabel('迭代次数');
ylabel('数值');
hold on;
% 开始迭代计算
while num ~= 1
% 迭代一次
if mod(num,2) == 0
num = num / 2;
else
num = num * 3 + 1;
end
iter = iter + 1;
% 绘图
plot(iter, num, 'ro');
pause(refresh);
hold on; % 这里的hold on命令也可省略
end
动态效果如下(暂时还没有录屏):

绘制多幅子图像
有些使用我们需要在同一张图中并列放置多张图像,这时候我们可以使用subplot进行绘制。其主要使用方法如下:
% 绘制m*n排列的子图像中的第p幅
subplot(m, n, p);
plot();
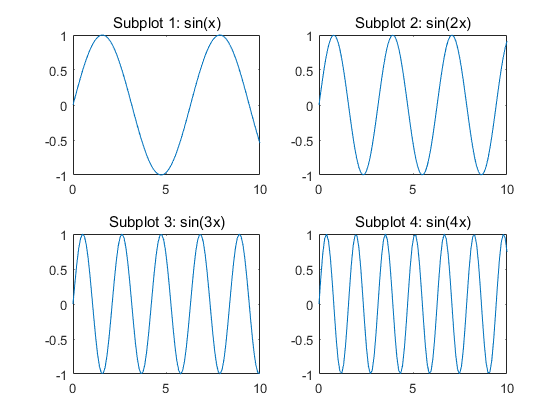
需要注意的是,subplot默认按逐行的方式对子图像进行排列。例如以下代码绘制了函数y=sin(k*x)在不同k值下的图像:
% 生成绘图数据
x = linspace(0,10);
y1 = sin(1*x);
y2 = sin(2*x);
y3 = sin(3*x);
y4 = sin(4*x);
% 绘制2*2排列的子图像
figure; % 第一次绘制时,figure命令可省略
subplot(2,2,1);
plot(x,y1);
title('Subplot 1: sin(x)');
subplot(2,2,2);
plot(x,y2);
title('Subplot 2: sin(2x)');
subplot(2,2,3);
plot(x,y3);
title('Subplot 3: sin(3x)');
subplot(2,2,4);
plot(x,y4);
title('Subplot 4: sin(4x)');
子图像的绘制结果如图所示: