新的算法专栏开始更新啦!这个专栏将介绍一些常用的经典算法。本次带来的是经典的串匹配算法——KMP算法。
串匹配算法
串匹配在实际使用中有着广泛的需求,从计算机领域简单的文本搜索,到生物科学领域复杂的氨基酸序列匹配,都离不开高效的串匹配方法。
KMP算法是经典的串匹配算法,由Knuth和Pratt师徒发明,同一时间Morris也发明了这一算法。因此按照姓氏首字母,这一算法得名“KMP”算法。简单而言,KMP算法主要通过根据对成功匹配段的复用以及对失败匹配段的学习来加快字符串匹配的速度,其时间复杂度为O(n)。
为方便下文的表述,我们作如下的约定:
- 文本串T(Text String):需要查询的全量字符串,其长度为n
- 模式串P(Pattern String):查询的片段字符串,其长度为m
- 匹配算法的结果为模式串在文本串中首次出现的位置(序号从0开始),不存在时应返回-1。
例如文本串T = "helloworldhello",模式串P = "ello",则匹配算法应返回1。
蛮力算法
字符串匹配的蛮力算法,可以将模式串逐一与文本串中长度为m的子串进行匹配。例如在文本串”abcabdab”中查找子串”abd”:
| 序号 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 文本串 | a | b | c | a | b | d | a | b | d |
| 匹配1 | a | b | |||||||
| 匹配2 | b | d | |||||||
| 匹配3 | b | d | |||||||
| 匹配4 | a | b | d |
其对应的暴力算法代码为(Java):
public int match(String P, String T) {
int n = T.length(); // 文本串长度
int m = P.length(); // 模式串长度
for (int i = 0; i < n - m + 1; i ++) { // 文本串中的起始查找位置
if (T.substring(i, i + m).equals(P)) return i; // 匹配子串
}
return -1;
}
为了披露更多的算法细节,这里我们不使用Java内置函数实现,以为接下来的KMP算法的理解做准备:
public int match(String P, String T) {
int n = T.length(), i = 0; // 文本串长度及当前比对字符
int m = P.length(), j = 0; // 模式串长度及当前比对字符
while ((i < n) && (j < m)) {
if (T.charAt(i) == P.charAt(j)) {
i ++; j ++; // 匹配,转到下一字符
} else {
i -= j - 1; j = 0; // 文本串回退,模式串复位
}
}
return (i - j > n - m) ? -1 : i - j; // 若匹配成功,则i-j表示匹配初始位置
}
很显然,蛮力算法由于需要对于每个子串进行比较,其时间复杂度在最差情况下为O(mn)。
蛮力算法的思考
再次回顾蛮力算法过程的例子:
| 序号 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 文本串 | a | b | c(i=2) | a | b | d | a | b | d |
| 匹配1 | a | b |
第一次匹配在i=2及j=2处失败后,文本串回退,模式串复位:
| 序号 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 文本串 | a | b(i=1) | c | a | b | d | a | b | d |
| 匹配2 | b | d |
很显然第二次匹配的时候同样失败了。那这个失败是偶然的吗?并不是。可以发现由于第一次匹配时已经成功匹配了字符串"ab",因此文本串一定是"abxxxxxx"。因此在i=1的位置,模式串一定不能和文本串进行匹配,因此这次失败是注定的。
KMP算法
为了使得已经成功的信息得到充分的利用,KMP算法对于“注定的失败”采取了聪明的避让措施,该算法的核心是next数组。
next数组
为了尽可能地利用已经匹配的信息,我们可以在安全的前提下,对模式串进行快速移动,而不是像暴力算法一样一次仅前进一格。很显然,模式串向右移动的距离之和自身有关,即无论何时,只要匹配到"abd"中的'd'失败后,就需要将模式串的j移动到next[j]的位置,称之为模式串P的next数组。
例如在上述的例子中,匹配到"abd"中的'd'失败后,我们知道当前位置的前两个字符一定为"ab",因此我们可以直接向右将模式串移动两位,即next[2] = 0,表示将j=2对应的’d’字符直接移动到’a’字符进行比对。这一比对过程为:
| 序号 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 备注 |
| 文本串 | a | b | c | a | b | d | a | b | d | |
| 匹配1 | a | b | j=2匹配失败,移动j=next[j]=0 | |||||||
| 移动模式串 | a(j=0) | b | d |
当文本串与模式串的第一个字符都不匹配时,模式串应当右移一位,继续和下一和文本串字符进行对比。为了统一起见,我们可以令next[0] = -1,表示当第0号字符不匹配时,需要将其移动到-1的位置,也即向右移动一位模式串。
通过上述例子,我们可以写出任意模式串的next数组,例如对于P = "chinchilla",其next表为:
| j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| T[j] | c | h | i | n | c | h | i | l | l | a |
| next[j] | -1 | 0 | 0 | 0 | 0 | 1 | 2 | 3 | 0 | 0 |
- j = 0时,匹配失败说明该位置的文本串与模式串的第一位不相等,此时应右移一位,即
next[0] = -1; - j = 1时,文本串中
"c"匹配成功,说明文本串格式为"cxxxx",应向右移动一位,即next[1] = 0; - j = 2时,文本串中
"ch"匹配成功,说明文本串格式为"chxxxx",应向右移动两位(因为如果只移动一位,文本串变为"hxxxx",模式串为"chin...",必然匹配失败),即next[2] = 0; - j = 3时,文本串中
"chi"匹配成功,说明文本串格式为"chixxxx",应向右移动三位,即next[3] = 0; - j = 4时,文本串中
"chin"匹配成功,说明文本串格式为"chinxxxx",应向右移动四位,即next[4] = 0; - j = 5时,文本串中
"chinc"匹配成功,说明文本串格式为"chincxxxx",此时我们发现如果将模式串右移四位,则文本串变为"cxxxx",与模式串"chin..."有可能匹配成功,因此next[5] = 1,即使得字符'h'移动到前面的'h'处; - …
- j = 8时,文本串中
"chinchil"匹配成功,说明文本串格式为"chinchilxxxx",此时我们必须将模式串右移8位,否则无论如何均不能与模式串"chinchilla"匹配成功,因此next[8] = 0; - …
通过上述方法,我们即可得到任意字符串的next数组。
KMP算法匹配
根据next数组的定义,我们可以很快写出KMP算法进行匹配计算的代码:
public int KMP(String P, String T) {
int n = T.length(), i = 0; // 文本串指针
int m = P.length(), j = 0; // 模式串指针
int[] next = buildNext(P); // 构建模式串P的next表
while ((j < m) && (i < n)) {
if ((j < 0) || (P.charAt(j) == T.charAt(i))) { // 匹配时,移动到下一字符
j ++; i ++;
} else { // 不匹配时,加速移动模式串
j = next[j];
}
}
return (i - j > n - m) ? -1 : i - j;
}
由于文本串指针永远不会后退,模式串指针只可能进行加1操作或者next操作(相等于做减法),因此该方法最多只可能进行2*n次操作,因此KMP算法中除next表构建外,其时间复杂度为O(n)。根据后续的分析,我们得到next表的构建最多需要O(m)时间,因此KMP算法的时间复杂度不超过O(m+n)。同时对于构建好的next表,只要模式串不发生变化,就可以连续不断使用,这也使得渐进复杂度接近于O(n)。
next数组的改进
当模式串P = "chinchilla"时,我们构造以下文本串T = "chincy...",其比对过程如下:
| 序号 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 备注 |
| 文本串 | c | h | i | n | c | y(i=5) | x | x | x | x | |
| 匹配1 | c | h | i | n | c | i | l | l | a | j=5匹配失败,j=next[j]=1 | |
| 移动模式串 | c | h(j=1) | i | n | c | h |
显然这次匹配也会失败,而这次失败也是必然的。我们发现,当模式串匹配到"chinch"而失败时,不仅说明此时文本串为"chincxxxx",同时还说明文本串中下一个字符必不为'h'。掌握这个细节,我们可以对next数组进行改进:
| j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| T[j] | c | h | i | n | c | h | i | l | l | a |
| next[j] | -1 | 0 | 0 | 0 | -1 | 0 | 0 | 3 | 0 | 0 |
- j = 4时,文本串中
"chin"匹配成功,'c'匹配失败,说明文本串格式为"chin[非c]xxxx",此时我们现如果将模式串右移4位,则文本串变为"[非c]xxxx",与模式串"chin..."仍然匹配失败,因此必须将模式串移动5位,即next[4] = -1(注意和改进前的区别); - j = 5时,文本串中
"chinc"匹配成功,'h'匹配失败,说明文本串格式为"chinc[非h]xxx",此时我们发现如果将模式串右移4位,则文本串变为"c[非h]xxx",与模式串"chin..."仍然匹配失败,因此必须将模式串移动5位,即next[5] = 0(注意和改进前的区别); - j = 7时,文本串中
"chinchi"匹配成功,'l'匹配失败,说明文本串格式为"chinchi[非l]xxxx",此时我们将模式串右移4位,文本串变为"chi[非l]xxxx",与模式串有概率匹配。因此next[7] = 3;
利用这种方式创建的next表,不仅可以从“成功”中获取经验,还可以从“失败”中获取教训,使得模式串可以尽可能快地移动。
next表构建分析
通过上述分析,我们已经对next表的计算方法有了一定的认知。总结来看,next表中next[j]的计算方法为:
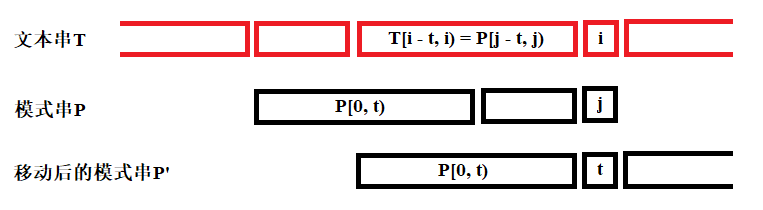
- 由于模式串匹配到j位时失败,因此对于模式串的前j-1位必然与文本串匹配,即
P[0, j) = T[i - j, i)。同时由于匹配失败,还可以得到P[j] ≠T[i]。 - 若我们下一轮匹配时,令T[i]和P[t]对齐,说明我们将模式串向右移动了j-t位。若此时能有与已知的文本串匹配,应有
P[0, t) = T[i - t, i],同时在P[t] ≠P[j]的情况下才有可能与T[i]进行匹配。 - 若存在很多组t,保险起见我们应当使得移动距离最小,因此需要使得
next[j] = max(t)。
归纳为数学语言如下:
next[j] = max({ t | P[0, t) = P[j - t, j) 且 P[t] ≠P[j] })
因此实质上,next表的构建是一个自我匹配的过程,仿照匹配代码,我们可以写出next表的构建代码:
public int[] buildNext(String P) {
int m = P.length();
int[] next = new int[m];
next[0] = -1; // 初始化next表
int t = -1, j = 0; // j为“主”串指针,t为移动串指针
while (j < m - 1) {
if ((t < 0) || (P.charAt(j) == P.charAt(t))) {
// 匹配的情况下,若后一元素不相等时才能移动到t,否则要直接移动到next[t]
j ++; t ++;
next[j] = (P.charAt(j) != P.charAt(t) ? t : next[t]);
} else { // 不匹配时,加速移动模式串
t = next[t];
}
}
return next;
}
这里可以看出来,当模式串进行移动的时候,只有next[t]才能成为候选者,因此利用已构建的部分next表,可以避免无用的移动。
手动计算next表
使用代码计算next表的过程很快,但是却不够直观。根据next表的数学定义,我们可以采用稍微繁琐,但是却非常直观地方式进行手动计算:
- 在第一行写上完整的模式串P,并标明其序号;
- 依次向右移动模式串,若可以匹配,则继续向后写,否则停止,并在后面标明首次失配位置indexT(首次失配位置在原串中的位置)和indexP(首次失配时在移动串中的位置)。需要注意的是,全匹配时,失配位置不存在;
- 查找next[j]时,由上向下查找indexT列,首次出现j值的行对应的indexP值即为next[j]。若不存在j值,则应填-1。
以"chinchillach"为例,手动计算其next表如下:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | indexT | indexP |
| c | h | i | n | c | h | i | l | l | a | c | h | ||
| c | 1 | 0 | |||||||||||
| c | 2 | 0 | |||||||||||
| c | 3 | 0 | |||||||||||
| c | h | i | n | 7 | 3 | ||||||||
| c | 5 | 0 | |||||||||||
| c | 6 | 0 | |||||||||||
| c | 7 | 0 | |||||||||||
| c | 8 | 0 | |||||||||||
| c | 9 | 0 | |||||||||||
| c | h | - | - | ||||||||||
| c | 11 | 0 |
根据上述表格,我们可以轻易得到next表的结果为:
| j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| P[j] | c | h | i | n | c | h | i | l | l | a | c | h |
| next[j] | -1 | 0 | 0 | 0 | -1 | 0 | 0 | 3 | 0 | 0 | -1 | 0 |
再以字符串"abababb"为例,其计算过程为:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | indexT | indexP |
| a | b | a | b | a | b | b | ||
| a | 1 | 0 | ||||||
| a | b | a | b | a | 6 | 4 | ||
| a | 3 | 0 | ||||||
| a | b | a | 6 | 2 | ||||
| a | 5 | 0 | ||||||
| a | 6 | 0 |
因此其next表为:
| j | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| P[j] | a | b | a | b | a | b | b |
| next[j] | -1 | 0 | -1 | 0 | -1 | 0 | 4 |
通过这两个例子,想必对于next表的手动计算也不会再害怕了。