二叉树是一种常用的数据结构,一般意义上对树的遍历均需要O(n)的时间复杂度和O(logn)的空间复杂度。本文将介绍一种O(1)空间复杂度的算法,这就是Morris树遍历算法。
二叉树的遍历
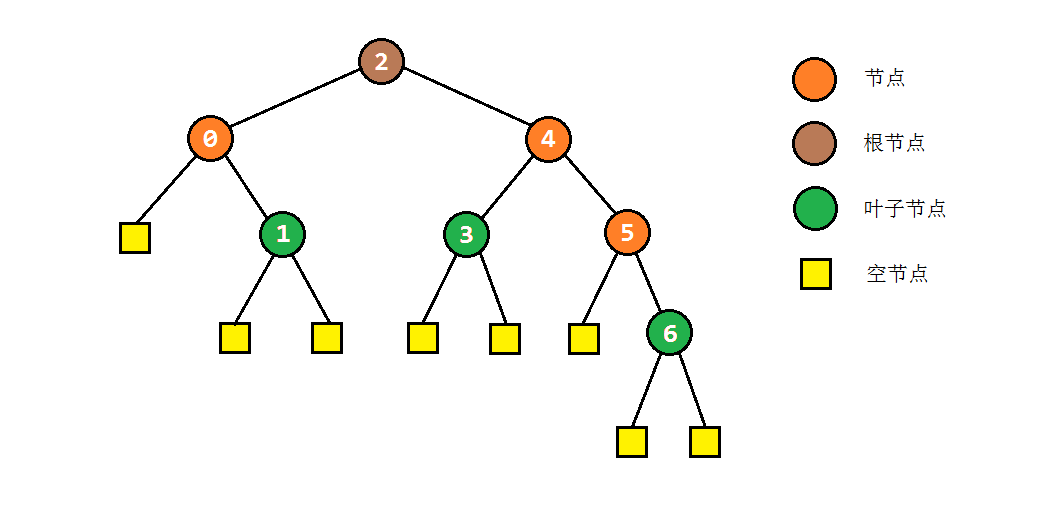
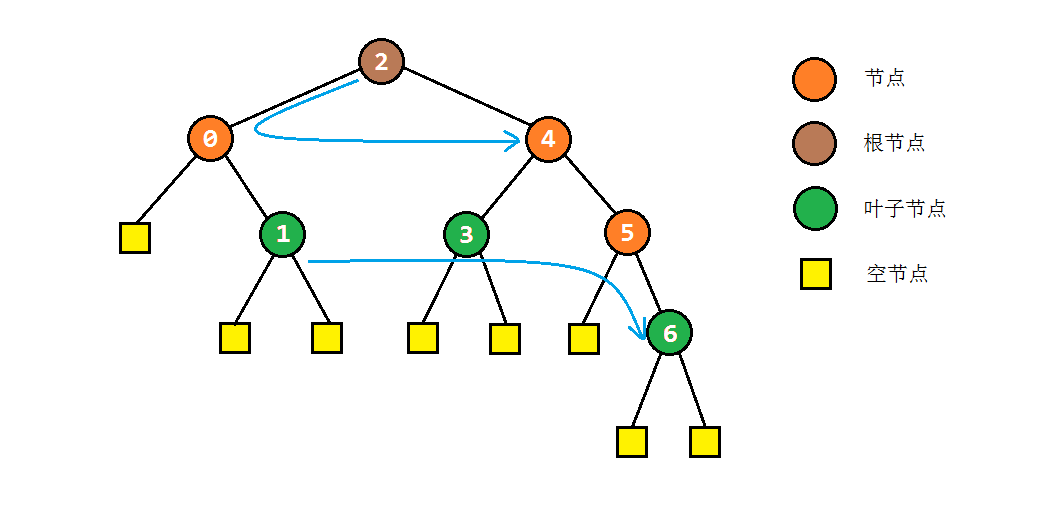
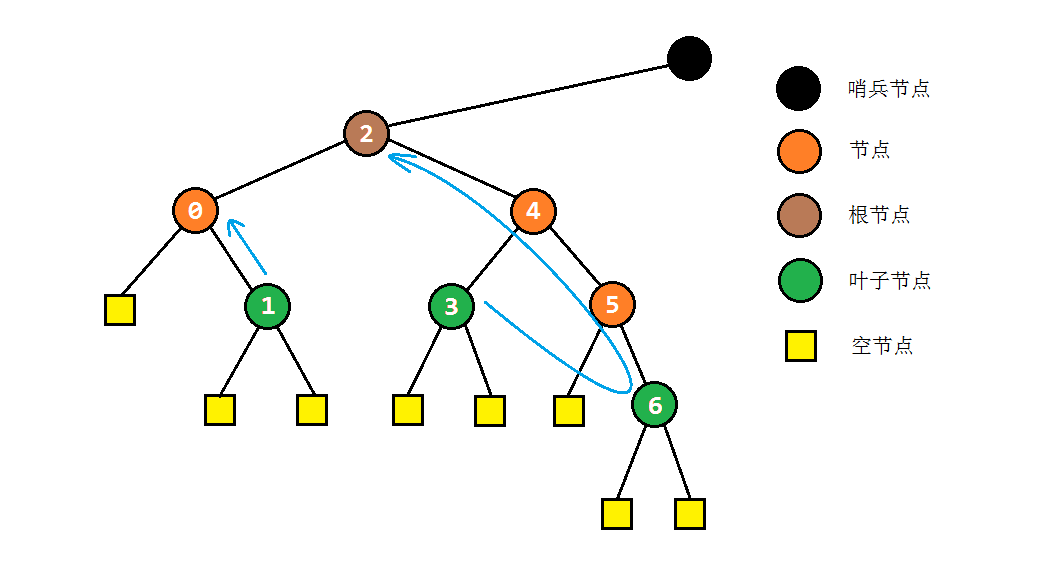
一般意义上来说,二叉树由很多个树节点构成的,非线性的数据结构。每个节点都拥有两个“子节点”,这个节点也被称之为子节点的“父节点”。通常地,我们称没有父节点的节点为“根节点”,两个子节点均为null的节点为“叶子节点”,如下图所示。
为统一起见,本文定义树节点的格式为:
class TreeNode {
public Value val; // 节点的值
public TreeNode left; // 左孩子
public TreeNode right; // 右孩子
}
而为了将这种非线性结构转化为线性结构使用,各种遍历顺序应运而生,一般包括:
- 先序遍历:按照
父节点 -> 左孩子 -> 右孩子的顺序遍历,与DFS(深度优先搜索)有一定联系; - 中序遍历:按照
左孩子 -> 父节点 -> 右孩子的顺序遍历。当二叉树为二叉搜索树时,中序遍历返回结果为有序序列,因此也叫顺序遍历; - 后序遍历:按照
左孩子 -> 右孩子 -> 父节点的顺序遍历。 - 层次遍历:从左到右,一层一层遍历整个树,与BFS(广度优先搜索)有一定联系。
递归遍历方法
利用递归处理二叉树的遍历问题非常方便,以先序遍历为例,其遍历方法如下:
public void preOrderTraversal(TreeNode root) {
if (root == null) return;
visit(root); // 访问节点
preOrderTraversal(root.left); // 访问左子树
preOrderTraversal(root.right); // 访问右子树
}
中序遍历、后序遍历与先序遍历类似,仅仅需要调整访问顺序即可。可以看出,递归方法的时间复杂度为O(n),空间复杂度与递归深度有关,最优情况与一般情况下为O(logn),最差情况下甚至需要O(n)的空间。
层次遍历利用递归则稍显复杂,在此不赘述。
非递归遍历方法
为使用非递归遍历方法遍历整个二叉树,往往需要借助栈/队列等数据结构辅助实现。
先序遍历
先序遍历的概念非常清晰,利用栈的辅助,在访问完该节点之后将子树入栈即可:
public void preOrderTraversal(TreeNode root) {
if (root == null) return;
Stack<TreeNode> stack = new Stack<TreeNode>(); // 利用栈进行临时存储
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop(); // 取出一个节点,表示开始访问以该节点为根的子树
visit(node); // 首先访问该节点(先序),之后顺序入栈右子树、左子树
if (node.right != null) stack.push(node.right);
if (node.left != null) stack.push(node.left);
}
}
或者使用如下方法,在节点到达null层时进行判断:
public void preOrderTraversal2(TreeNode root) {
if (root == null) return;
Stack<TreeNode> stack = new Stack<TreeNode>(); // 利用栈进行临时存储
TreeNode node = root;
while (!stack.isEmpty() || node != null) { // stack为空且node为null时,说明已经遍历结束
if (node != null) { // 可以深入左孩子时,先访问,再深入
visit(node);
stack.push(node);
node = node.left;
} else { // 否则深入栈中节点的右孩子
node = stack.pop().right;
}
}
}
以之前的树为例,其先序遍历结果应为:2 -> 0 -> 1 -> 4 -> 3 -> 5 -> 6
中序遍历
中序遍历的思想是:
- 若节点还有左子树,就要先把左子树访问完
- 没有左子树可访问时,访问该节点,并尝试访问右子树
按照这种思路,我们可以写出一种直接的方法:
public void inOrderTraversal(TreeNode root) {
if (root == null) return;
Stack<TreeNode> stack = new Stack<TreeNode>(); // 利用栈进行临时存储
TreeNode node = root;
while (node != null) { // 当node为null时,说明已经遍历结束
if (node.left != null) { // 存在左子树时,入栈并深入左子树
stack.push(node);
node = node.left;
} else { // 否则就寻找可以深入右子树的节点
while (!stack.isEmpty() && node.right == null) {
// 对于不能深入右子树的节点:直接访问,此时子树访问结束
visit(node);
node = stack.pop();
}
visit(node); // 如果可以深入右子树,访问该节点后,深入右子树
node = node.right;
}
}
}
或者根据先序遍历方法2进行修改,在节点出栈时访问节点:
public void inOrderTraversal2(TreeNode root) {
if (root == null) return;
Stack<TreeNode> stack = new Stack<TreeNode>(); // 利用栈进行临时存储
TreeNode node = root;
while (!stack.isEmpty() || node != null) { // stack为空且node为null时,说明已经遍历结束
if (node != null) { // 可以深入左孩子
stack.push(node);
node = node.left;
} else { // 否则访问栈中节点,并深入右孩子
node = stack.pop();
visit(node);
node = node.right;
}
}
}
以之前的树为例,其中序遍历结果应为:0 -> 1 -> 2 -> 3 -> 4 -> 5 -> 6
后序遍历
后序遍历从想法上是最难实现的,其主要思想是:
- 尝试按顺序访问该节点的左右子树
- 当左右子树都访问完毕时,才可以访问该节点
因此可以考虑采用栈的方式,依次将根节点、右孩子、左孩子入栈,以保证访问次序。由于后续遍历的回溯过程只可能上升一层,因此可以添加临时变量lastNode记录刚刚访问的节点,如果当前节点是上次访问节点的父节点,则说明子树访问完成,可以访问当前节点了。
public void postOrderTraversal(TreeNode root) {
if (root == null) return;
Stack<TreeNode> stack = new Stack<TreeNode>(); // 利用栈进行临时存储
stack.push(root);
TreeNode lastNode = root; // 为了判断父子节点关系
while (!stack.isEmpty()) {
TreeNode node = stack.pop(); // 取出一个节点,表示开始访问以该节点为根的子树
if ((node.left == null && node.right == null) || // 如果该节点为叶子节点
(node.left == lastNode || node.right == lastNode)) { // 或者已经访问过该节点的子节点
visit(node); // 直接访问
lastNode = node;
} else { // 否则就按顺序把当前节点、右孩子、左孩子入栈
stack.push(node);
if (node.right != null) stack.push(node.right);
if (node.left != null) stack.push(node.left);
}
}
}
当然,对上述方法的一个修改是添加“哨兵”节点,用于判断回溯位置。不过显然这种方式还需要对一些方法进行添加,并不是特别“优雅”:
public void postOrderTraversal2(TreeNode root) {
if (root == null) return;
Stack<TreeNode> stack = new Stack<TreeNode>(); // 利用栈进行临时存储
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop(); // 取出一个节点,表示开始访问以该节点为根的子树
if (!node.isValid()) { // 判断是“哨兵”节点,说明之后的节点为父节点,可以直接访问
node = stack.pop();
visit(node);
} else if ((node.left == null && node.right == null)) { // 如果该节点为叶子节点,也可直接访问
visit(node);
} else { // 否则就按顺序把当前节点、“哨兵”节点、右孩子、左孩子入栈
stack.push(node);
stack.push(new TreeNode(new Value(Value.INVALID_VALUE)));
if (node.right != null) stack.push(node.right);
if (node.left != null) stack.push(node.left);
}
}
}
以之前的树为例,其后序遍历结果应为:1 -> 0 -> 3 -> 6 -> 5 -> 4 -> 2
层次遍历
相较于前面几种遍历方式,层次遍历是最直观的遍历方式,可以利用队列来辅助实现:
public void levelTraversal(TreeNode root) {
if (root == null) return;
Queue<TreeNode> queue = new LinkedList<TreeNode>(); // 利用队列进行临时存储
queue.offer(root);
while(!queue.isEmpty()) { // 取出一个节点,并将其左右节点入列
TreeNode node = queue.poll();
visit(node);
if (node.left != null) queue.offer(node.left);
if (node.right != null) queue.offer(node.right);
}
}
可以看到,层次遍历和先序遍历相比,只是将栈换成了队列,其余处理方式完全相同。以之前的树为例,其层次遍历结果应为:2 -> 0 -> 4 -> 1 -> 3 -> 5 -> 6
复杂度分析
很显然,无论哪种遍历方式,一个节点最多只可能被访问两次,因此其时间复杂度均为O(n)。而由于借助了栈和队列这样的辅助数据结构,其空间复杂度与树高有直接关系,因此其空间复杂度为最好和平均O(logn),最差O(n),与递归方式的实现相同。
Morris遍历
主要思想
Morris遍历方法打破了一般遍历思想上的“禁锢”,通过临时对子节点引用的修改来实现“后继”节点的保存,之后再次遍历到时可以恢复树的结构,以此仅仅通过O(1)的空间实现树的遍历。没错,这又是KMP算法里面的Morris发明的(为什么别人可以这么聪明……)
我们先以中序遍历为例,介绍Morris算法的核心思想。回顾一下中序遍历的内容:
- 若节点还有左子树,就要先把左子树访问完
- 没有左子树可访问时,访问该节点,并尝试访问右子树
之前我们还提到过,如果这棵树是一棵二叉搜索树,那么中序遍历的结果应当是一个有序数组。为了方便起见,我们可以按照中序遍历的结果,将整个树组成一个链表,每一个节点都有“前驱”节点和“后继”节点。例如在之前示例的二叉树上,0是1的前驱节点,而2是1的后继节点。
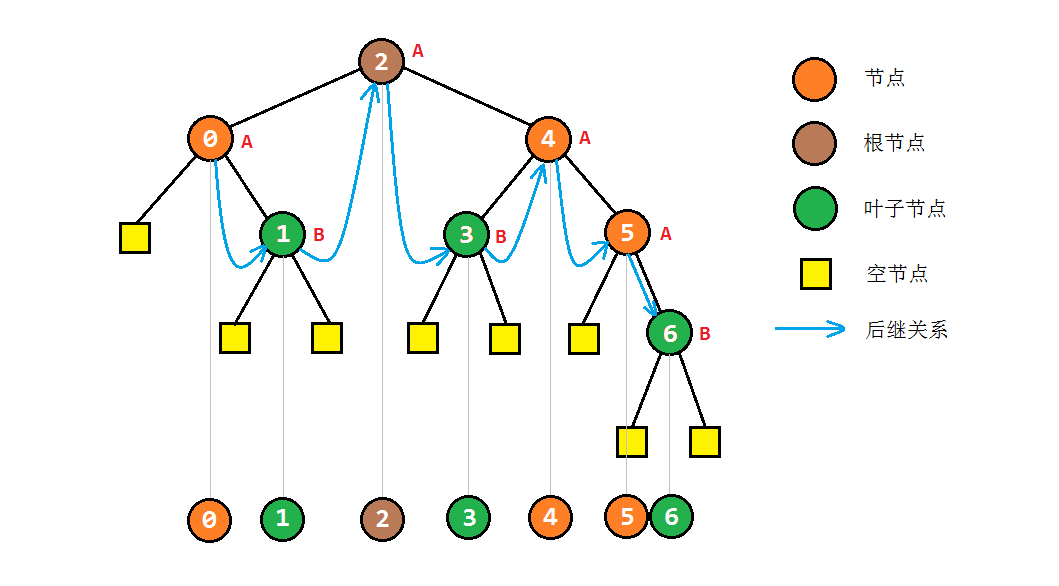
显然,中序遍历可以转化为对后继节点的计算过程。后继节点的计算方法为:
1. 对于存在右子树的节点A,其后继节点是其右子树中最左侧的节点;
2. 对于没有右子树的节点B,其后继节点是其自下而上的父节点中第一个将其作为左子树的节点。
节点A的后继计算非常简单。然而由于二叉树的信息中不包括父节点的信息,因此第2条操作起来非常困难,这也是为何之前采用了栈/队列的方式存储父节点的信息。
但是我们注意到,虽然对于这样的节点B,求取其后继节点非常困难;但是其后继节点来说,由于节点B是其子树中的一个节点,因此求前驱节点就很容易了!为了使得访问到节点B时能够直接得到后继信息,我们可以暂时使用B节点右子树的链接,存储后继节点,以实现对后继节点的直接获取,同时不占用额外的空间。这就是Morris遍历算法的主要思想。
Morris中序遍历算法
根据上述分析,我们可以写出程序的主要计算过程:
- 从根节点开始访问。
- 如果当前节点C不存在左子树,按中序遍历的规则,应当访问节点C,并进入其右子树进行遍历。
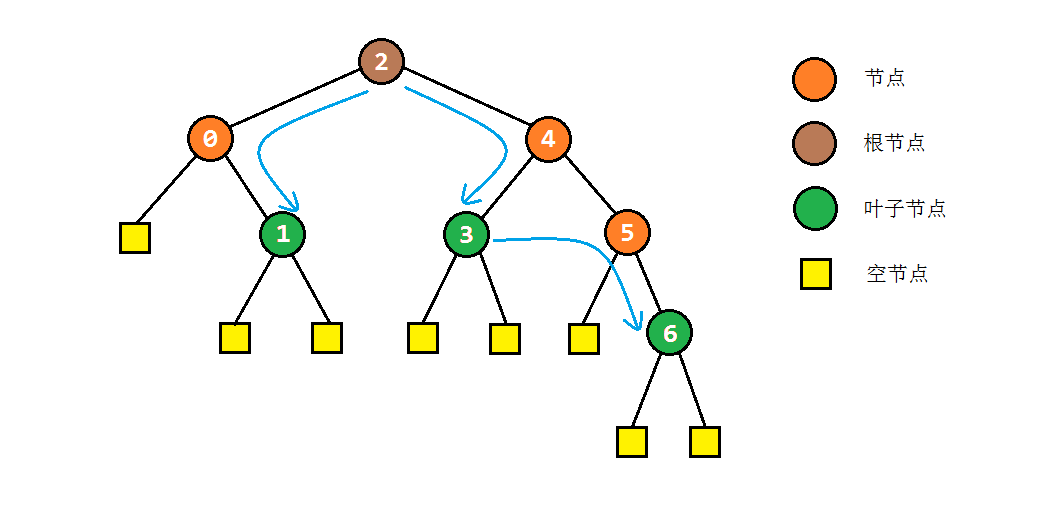
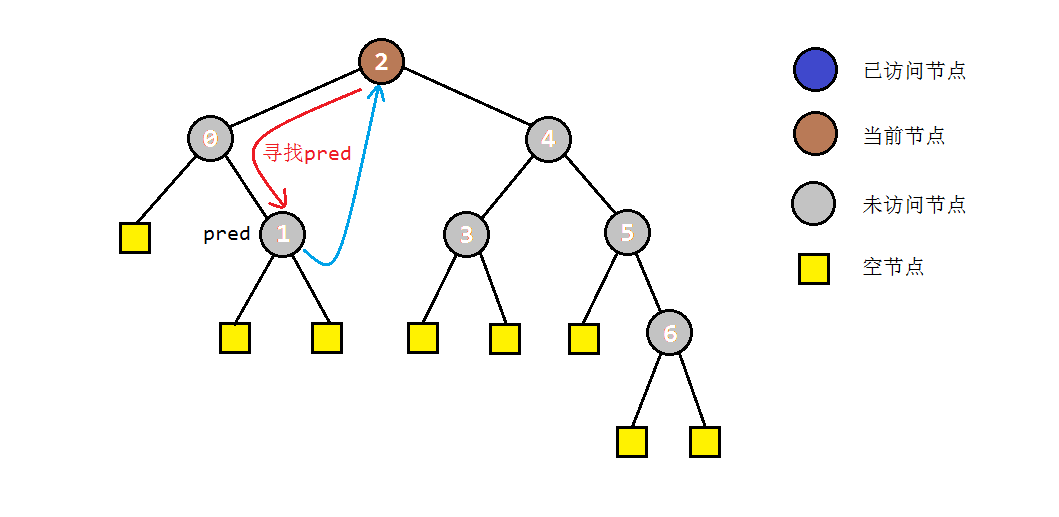
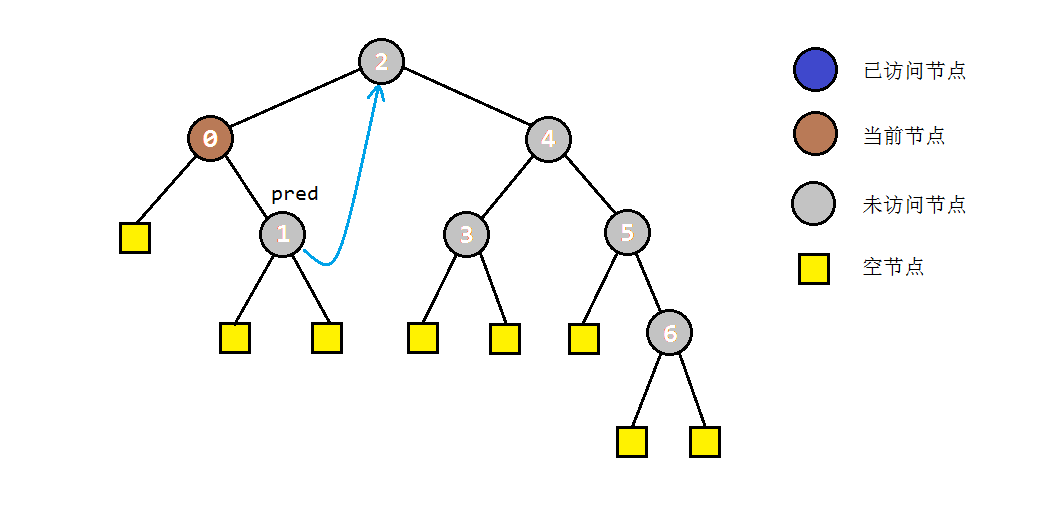
- 如果当前节点C存在左子树,就找到C的前驱节点B,并将B的右孩子指向C(存储后继),同时当前节点转入左子树进行遍历。
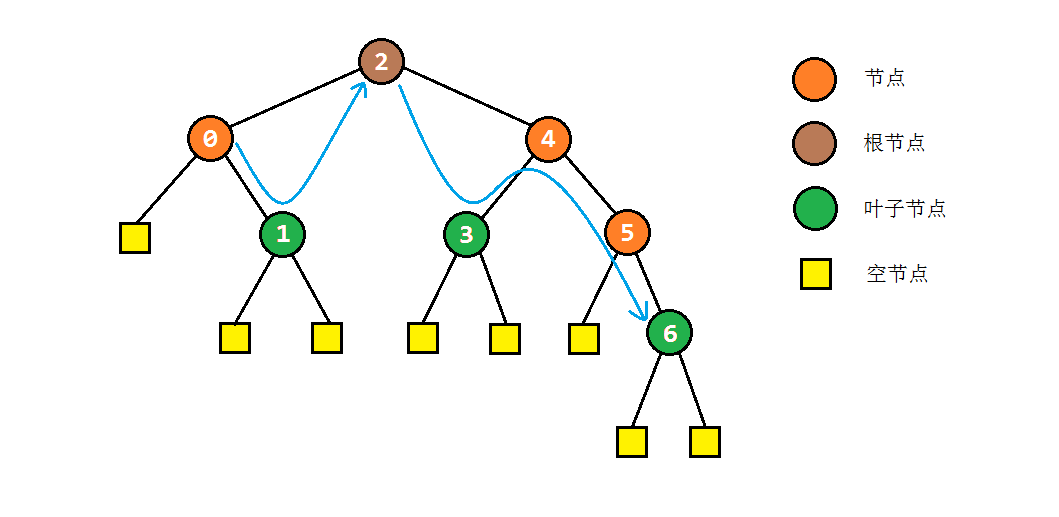
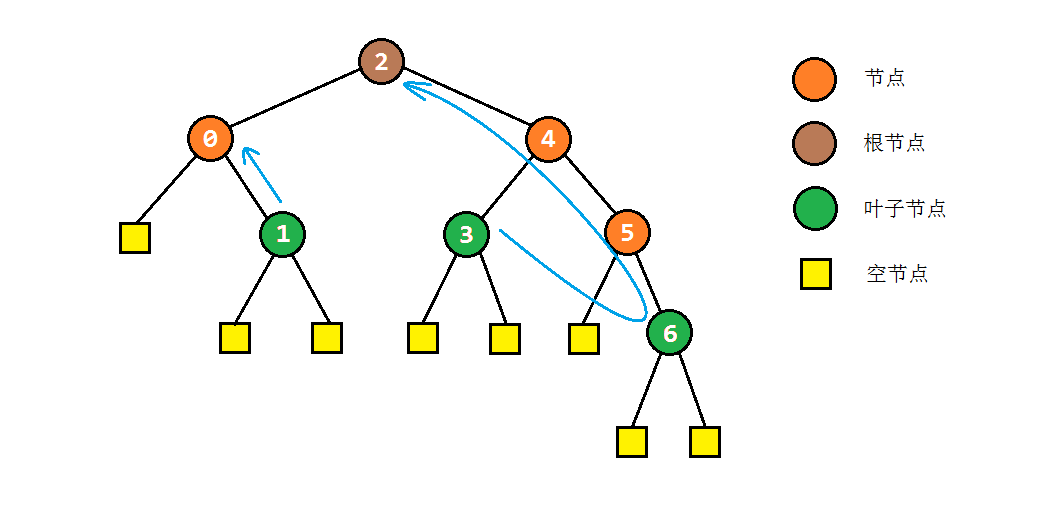
- 步骤2中访问右子树时,如果节点本身没有右子树,则会直接转入其后继节点C。根据中序遍历的规则,说明此时C的左子树遍历完成。为了还原树结构,我们需要重新找到C的前驱节点,并将其右孩子设置为null。之后我们访问节点C,并进入其右子树进行遍历。
以之前的示例树为例,图解一下morris遍历的部分过程:
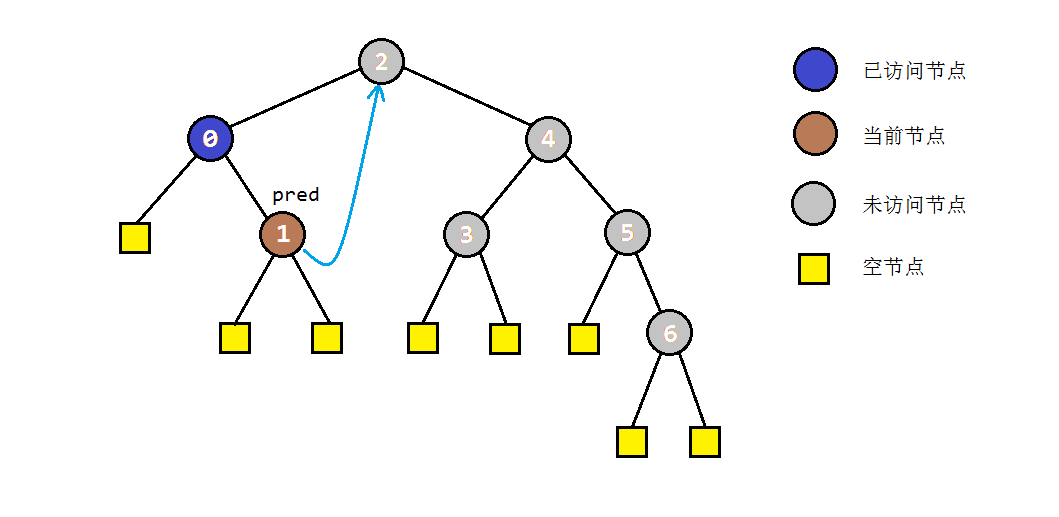
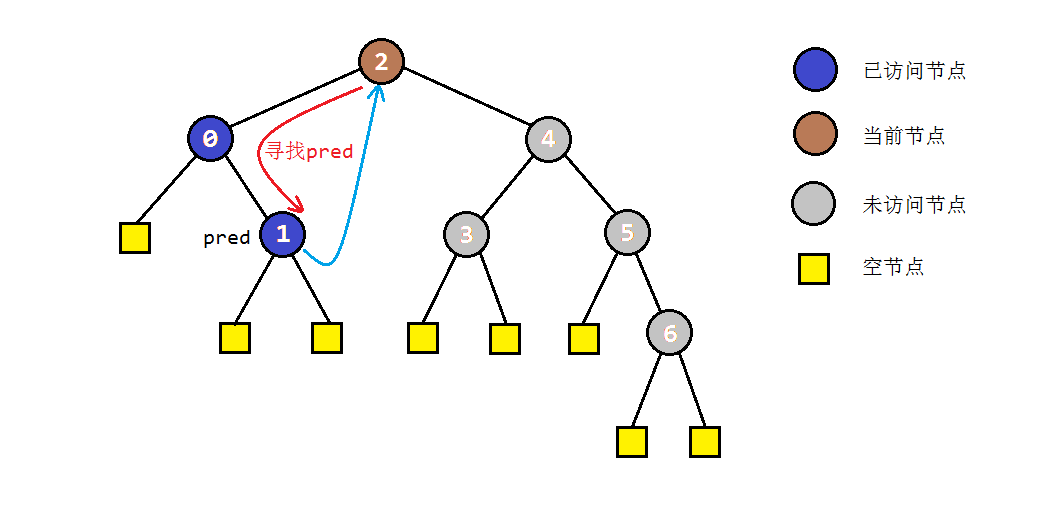
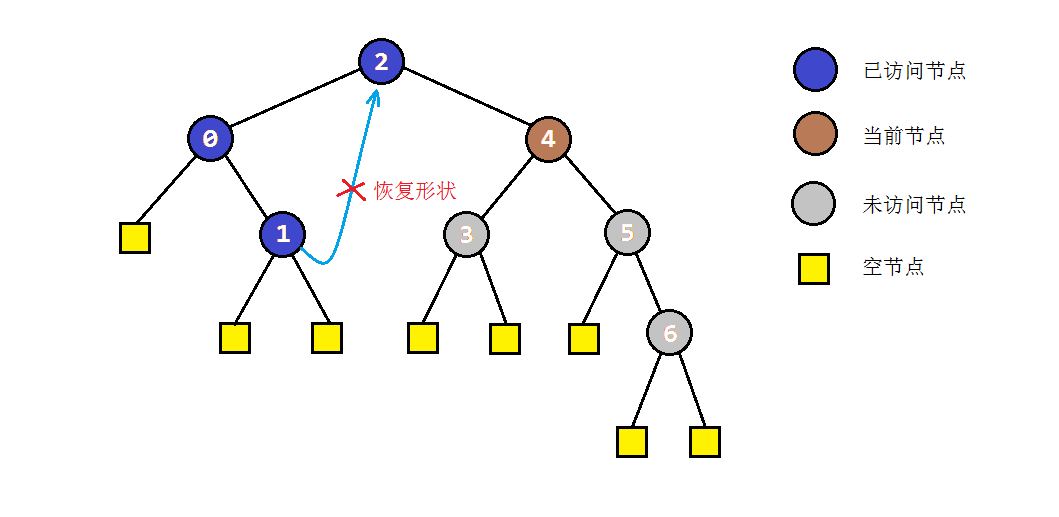
因此,我们写出Morris中序遍历算法的程序如下:
public void morrisInOrderTraversal(TreeNode root) {
TreeNode node = root, prev = null; // 仅存放两个临时变量,O(1)空间复杂度
while (node != null) { // 当前节点为空时,说明访问完成
if (node.left == null) { // 左子树不存在时,访问+进入右节点
visit(node);
node = node.right;
} else { // 左子树存在,寻找前驱节点。注意寻找前驱节点时,会不断深入右子树。不加判断时,若前驱节点的右子树已指向自己,会引起死循环
prev = node.left;
while (prev.right != null && prev.right != node) prev = prev.right;
if (prev.right == null) { // 前驱节点未访问过,存放后继节点
prev.right = node;
node = node.left;
} else { // 前驱节点已访问过,恢复树结构
visit(node); // 确定访问过左子树后,访问当前节点
prev.right = null;
node = node.right;
}
}
}
}
其中最关键的一步是判断前驱节点是否访问过。注意到如果前驱节点访问过,则其右孩子必然为当前节点,否则必然为空。据此可以判断应当深入左子树还是右子树。
复杂度分析
O(1)的空间复杂度是毋庸置疑的,但是该算法是否与普通的遍历算法具有相同的时间效率?我们对时间复杂度进行简要的分析。
整个计算过程中,我们可以看到,主要的复杂度为计算前驱的循环,这里的复杂度与树高有直接关系,一般为O(logn)。但这是否说明Morris遍历的复杂度为O(nlogn)呢?仔细分析后发现,对于每一个有左子树的节点,其寻找前驱的过程只会执行两次,一次是建立前驱-后继关系的时候,一次是恢复树结构的时候。因此事实上,二叉树的每条路最多只可能被循环访问两次,其时间复杂度必然为O(n)。
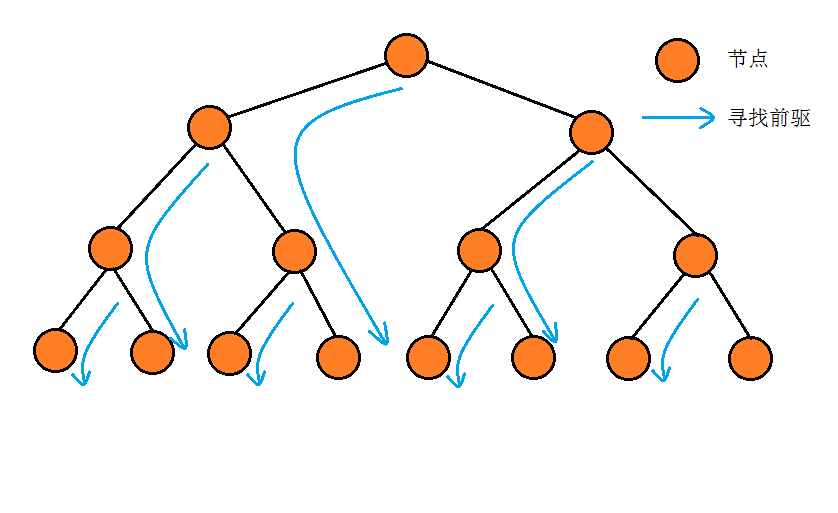
当然,我们也可以逐层计算循环总计算次数。例如对于一棵满二叉树,其倒数第二层的节点树为n/4,寻找前驱的长度为2,以此类推,我们可以得到:
\[C = \sum_{i=1}^{\log_2(n/2)} \frac{n}{2^{i+1}} \times i = \frac{n}{4} \times 1 + \frac{n}{8} \times 2 + \frac{n}{16} \times 3 + \cdots + 1 \times \log_2(\frac{n}{2}) = n - 1 - \log_2(n) \sim O(n)\]Morris先序遍历与后序遍历算法
介绍完了Morris中序遍历,其先序遍历和后序遍历都是在中序遍历的基础之上加以改动得到的。例如先序遍历时,需要先访问节点,再决定深入左子树或右子树:
public void morrisPreOrderTraversal(TreeNode root) {
TreeNode node = root, prev = null; // 仅存放两个临时变量,O(1)空间复杂度
while (node != null) { // 当前节点为空时,说明访问完成
if (node.left == null) { // 左子树不存在时,访问+进入右节点
visit(node);
node = node.right;
} else { // 左子树存在,寻找前驱节点。注意寻找前驱节点时,会不断深入右子树。不加判断时,若前驱节点的右子树已指向自己,会引起死循环
prev = node.left;
while (prev.right != null && prev.right != node) prev = prev.right;
if (prev.right == null) { // 前驱节点未访问过,存放后继节点
visit(node); // 在确定前驱节点未访问过时,访问当前节点(注意与中序遍历的区别)
prev.right = node;
node = node.left;
} else { // 前驱节点已访问过,恢复树结构
prev.right = null;
node = node.right;
}
}
}
}
后序遍历相比中序遍历稍微复杂一些,但是后序遍历也有其特性:若一个节点是右孩子,或该节点是左孩子但是没有兄弟节点,则访问完该节点后立刻会访问该节点的父节点。
推广到Morris遍历里,可以得到:
当访问到任何节点C的前驱节点B时,由B到C的路径(不包括节点C)即为之后的访问顺序。
因此所有的访问过程可以化为由B到C的访问。得到的Morris后序遍历程序如下,注意为了保证程序能够顺利访问右子树,为根节点添加了一个哨兵节点:
public void morrisPostOrderTraversal(TreeNode root) {
TreeNode temp = new TreeNode(new Value(Value.INVALID_VALUE)), node = temp, prev = null; // 仅存放一个“哨兵”节点和两个临时变量,O(1)空间复杂度
temp.left = root;
while (node != null) { // 当前节点为空时,说明访问完成
if (node.left == null) { // 左子树不存在时,进入右节点
node = node.right;
} else { // 左子树存在,寻找前驱节点。注意寻找前驱节点时,会不断深入右子树。不加判断时,若前驱节点的右子树已指向自己,会引起死循环
prev = node.left;
while (prev.right != null && prev.right != node) prev = prev.right;
if (prev.right == null) { // 前驱节点未访问过,存放后继节点
prev.right = node;
node = node.left;
} else { // 前驱节点已访问过,恢复树结构
visitReverse(node.left, prev); // 确定访问过左子树后,逆序访问沿路节点(注意与中序遍历的区别)
prev.right = null;
node = node.right;
}
}
}
}
对于逆序访问函数visitReverse(),我们可以采用链表翻转的方式实现,一个参考实现如下:
public void visitReverse(TreeNode node1, TreeNode node2) {
reverse(node1, node2); // 首先进行翻转
TreeNode node = node2; // 之后进行顺序访问
while (node != node1) {
visit(node);
node = node.right;
}
visit(node1);
reverse(node2, node1); // 恢复结构
}
public void reverse(TreeNode node1, TreeNode node2) {
// 实现链表翻转
TreeNode prev = node1;
TreeNode current = prev.right;
TreeNode next = current.right;
while (prev != node2) {
current.right = prev;
prev = current;
current = next;
next = next.right;
}
}
以此实现后序遍历结果。由于相比较其他两种遍历,后序遍历多了逆序访问的过程,其时间复杂度与链表长度成正比。因此后序遍历的时间复杂度仍然为O(n)。