在SIF的招募设定中,可以选择单抽(5心抽1张)以及11连(50心抽10张)这样两种抽卡方式。本文将通过计算,分析在100box(即共计100张的无放回抽卡卡池)中如何尽可能节省资源。
1. 计算背景与设定
1.1 问题描述
假设卡池中共有100张卡,只有1张为我们需要的“UR卡”。现在对其进行不放回随机抽卡。我们每次可以采用两种抽取策略的任意一种:
- 花费50心,抽11张卡;
- 花费5心,抽1张卡。

显然在刚开始抽卡时,使用50心抽11张卡的方案较优(平均4.5心一抽)。而随着抽卡逐渐进行到最后,UR的概率逐渐提高,11连往往会“浪费”一些心:极端情况下,当卡池仅剩11张卡时,11连方案需要50心才能获取到UR,而单抽方案则平均只需要6抽(即30心)即可获取到UR。因此我们需要制定一个策略来实现最节省资源的抽卡:在卡池里的卡数一个特定数值时,采用11连,随后均采用单抽。
因此我们的待求问题为:如何确定N的值,在剩余卡数量大于N时,采用11连,否则采用单抽。
【补充说明】
考虑到红券、绿券对于不同卡池的效用不同,关于其是否可以等效为50心与5心的问题将在2.4中进行补充说明。此模型仅考虑用心抽卡池的情况。
1.2 问题分析与简化
首先需要明确的是,对于一个无放回的抽卡来说,若100抽的box抽到剩N抽时还未抽到UR,则剩余box的抽卡体验等同于抽一个仅有N抽的box。因此我们不妨假设,卡池中仅有N张卡,且只有1张UR,那么针对接下来的11抽,是应该选择11连还是单抽?
简化后的问题与原问题具有等价性,这是由于:
若简化问题中单抽方式占优,则恰好对应原问题中利用单抽的方式;若简化问题中11连占优,说明可抽一次11连,并转化为当N'=N-11时的简化问题。初始时N为100,最终必将在一个特定的N值上两种策略效用相等。
我们待求问题转换为:如何确定N的值,使得在一个仅剩N抽的box中,使用50心进行11连,和使用55心进行11次单抽,平均花费的心数相等?
2. 问题分析与求解
2.1 问题求解
在100box的抽卡中,累积抽卡次数和出货概率之间的关系显然是线性的:
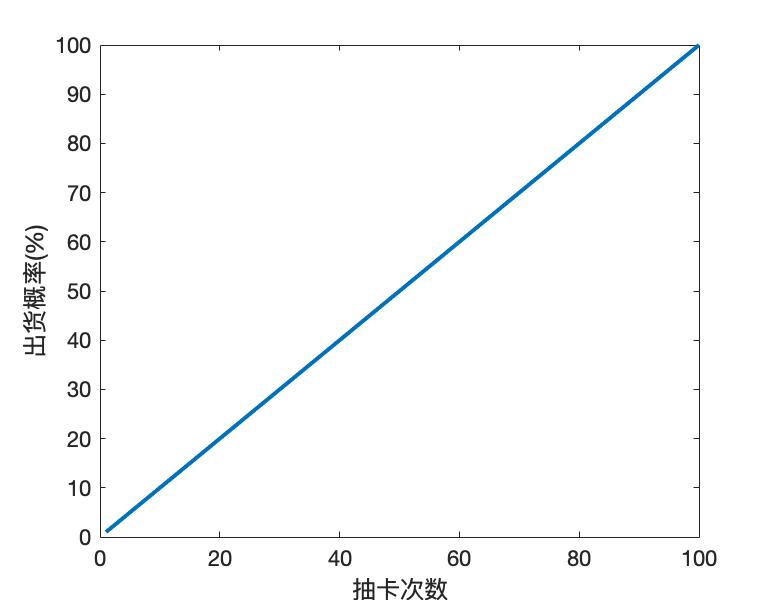
我们假设,当卡池剩余N张卡时,在某个特定策略下,为了抽到UR,期望花费的心数是E(N)。由于我们仅考虑接下来11抽的抽卡策略,因此我们可以使得11抽后的E(N-11)为一个定值。那么我们分别采用方案1(11连)和方案2(11次单抽),则:
-
方案1:如果在11连中抽到,则花费
50心;如果11连中没有抽到,则花费50+E(N-11)心; -
方案2:如果在11次单抽中抽到,因为是随机出现在任意一次中,期望花费
30心;如果11连中没有抽到,则花费55+E(N-11)心。
显然,box的特定保证了我们在为了11次抽卡中,能抽到UR的概率为:P_11 = 11/N。因此,两种方案下抽到UR消耗心数的期望分别是:
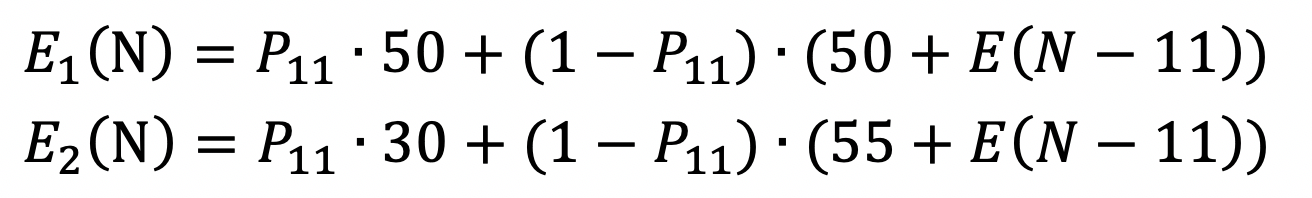
二者期望相同时即为分界点,因此得到:
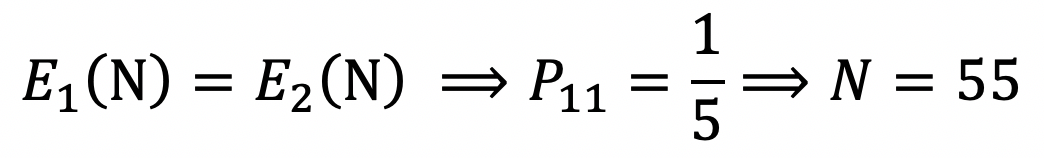
由此我们得到结论:在卡池剩余张数大于55张时,应使用11连,否则应使用单抽。
2.2 模拟验证
2.2.1 期望模拟
以上的分析从理论上得到了一个初步结论,那么接下来我们通过模拟的方式对结果进行验证。
用matlab模拟了一亿次box抽卡,分别采用不同的十一连次数策略,即前若干次抽卡用11连,之后转为单抽,得到的期望心数花费如下图所示:、
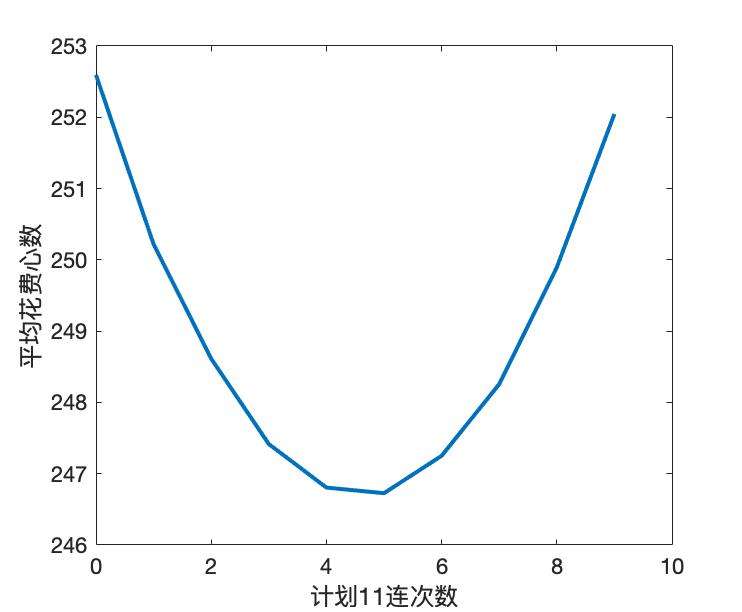
可见,前四次11连或前5次11连,即剩余张数为56/45时,平均花费的心数基本都是最低的,这也与我们计算的结果相吻合。不过同时也可以看到,即使是全部单抽这种“土豪行径”,从模拟结果上也只比最优策略多花了5.87心,所以千辛万苦,也就省下了一次单抽的资源。
2.2.2 风险模拟
同样的,我们也可以对不同抽卡策略进行“风险分析”,即采用不同策略下平均抽卡花费心数的标准差:
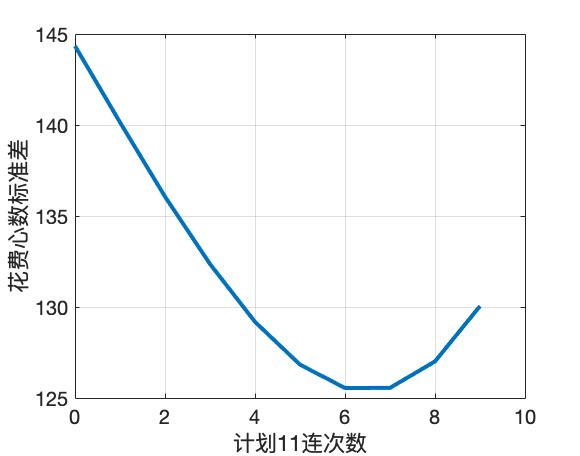
图中看来的话,先抽5次11连这种方案,花费心数的标准差为127心,所以这种策略是一种期望又高,风险又较低的抽卡方式。
2.3 该结果的适用条件
仅适用于你资源足够,且必须要抽出UR的情况。
【以下两种条件不再适用】
- 资源不够一盒box又想要:氪金氪得越多越便宜,不再适用于5心与50心的比例,因此只管11连就完了,后面氪金能少一点。
- 随便抽着玩,不一定要抽出来:问题转化为UR期望问题,同样也是只管11连就完了
2.4 其他讨论
2.4.1 红券是否应该优先使用?
从作用上来说,券只能抽box与无限池,不能抽阶梯,一定程度上限制了券的使用。因此红券抽box时可以先使用,因为其和50心在box和无限池中完全等价。
2.4.2 绿券应该在无限池中还是box中使用?
绿券众所周知是不适合抽无限池的,如下图展示了绿券抽box和无限池得到的期望UR数及0UR概率:
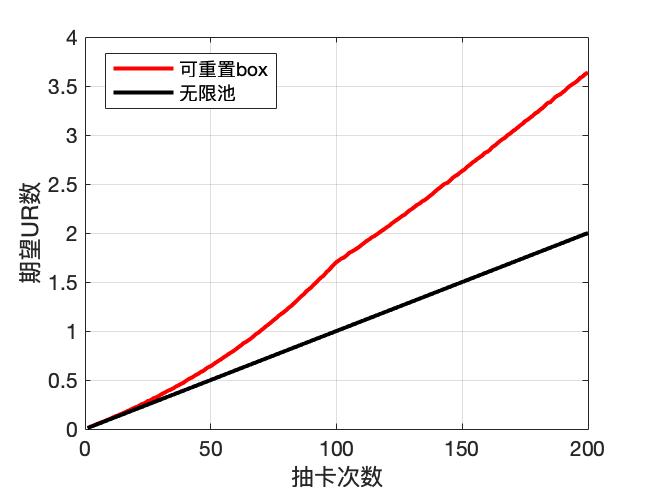
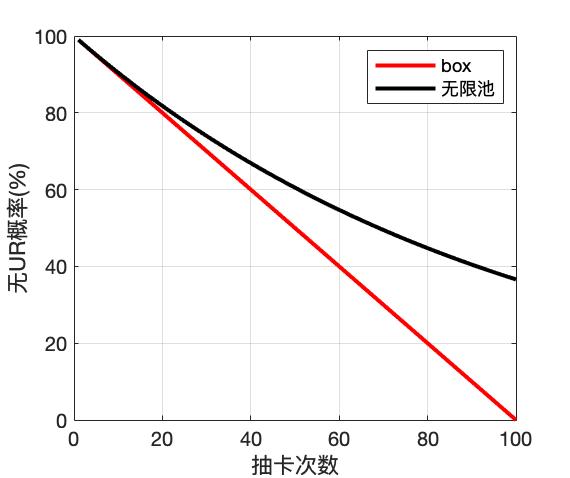
可见绿券无论从任何角度来说都应该投入到box中,而不是无限池。很有意思的地方是,在可重置box中,期望UR数在低于100抽时是一个下凹的曲线,而在大于100抽后则变为一条过原点的直线,这点后面如果有时间可以探讨下该形状形成的原因。
2.4.3 绿券是否应该优先使用?
这和个人的绿券数量和抽卡计划有关,即需要确定当前绿券是否溢出。手上绿券多,又没有什么抽box的计划时,绿券几乎完全没有作用,因此完全可以将绿券优先投入box使用。而如果能保证手上绿券只抽box都不够的情况下,则可以等同于本文中的5心,即4次或5次11连后再使用绿券掏底。
3. 结论
在100box中:
1. 为尽可能节省爱心,卡池剩余数量大于55张时,应使用11连,否则应使用单抽(即先进行4次或5次11连后单抽),但不同方案平均差距不超过6心;
2. 为尽可能避免风险,可以选择6次或7次11连后,使用单抽;综合考虑1,最佳方案是进行5次11连,此时平均花费爱心数为:247±127;
3. 红券可以视为50心在box中使用;绿券应该尽可能仅在box中使用,在绿券溢出时,可以优先使用绿券抽box,否则应该视为5心使用。